Introduction
Contents

Introduction¶
Why do we have to learn mathematics? - This is a question I am asked and think about almost every day.
On the surface, advanced mathematics doesn’t impact software engineering and machine learning in a production setting. You don’t have to calculate gradients, solve linear equations, or find eigenvalues by hand. Basic and advanced algorithms are abstracted away into libraries and APIs, performing all the hard work for you.
Nowadays, implementing a state-of-the-art deep neural network is almost equivalent to instantiating an object in TensorFlow, loading the pre-trained weights, and letting the data blaze through the model. Just like all technological advances, this is a double-edged sword. On the one hand, frameworks that accelerate prototyping and development enable machine learning in practice. Without them, we wouldn’t have seen the explosion in deep learning that we witnessed in the last decade.
On the other hand, high-level abstractions are barriers behind us and the underlying technology. User-level knowledge is only sufficient until one is treading on familiar paths. (Or until something breaks.)
If you are not convinced, let’s do a thought experiment! Imagine moving to a new country without speaking the language and knowing the way of life. However, you have a smartphone and a reliable internet connection.
How do you start exploring?
With Google Maps and a credit card, you can do many awesome things there: explore the city, eat in excellent restaurants, have a good time. You can do the groceries every day without speaking a word: just put the stuff in your basket and swipe your card at the cashier.
After a few months, you’ll start to pick up some language as well—simple things like saying greetings or introducing yourself. You are off to a good start!
There are built-in solutions for everyday tasks that just work—food ordering services, public transportation, etc. However, at some point, they will break down. For instance, you need to call the delivery person who dropped off your package at the wrong door. This requires communication.
You may also want to do more. Get a job, or perhaps even start your own business. For that, you need to communicate with others effectively.
Learning the language when you plan to live somewhere for a few months is unnecessary. However, if you want to stay there for the rest of your life, it is one of the best investments you can make.
Now replace the country with machine learning and the language with mathematics.
Fact is, algorithms are written in the language of mathematics. To work with algorithms on a professional level, you have to speak it.
What is this book about?¶
There is a similarity between knowing one’s way about a town and mastering a field of knowledge; from any given point one should be able to reach any other point. One is even better informed if one can immediately take the most convenient and quickest path from the one point to the other. — George Pólya and Gábor Szegő, in the introduction of the legendary book Problems and Theorems in Analysis
The above quote is one of my all-time favorites. For me, it implies that knowledge rests on many pillars. Like a chair has four legs, a well-rounded machine learning engineer also has several skills that enable them to be effective in their job. Each of us focuses on a balanced constellation of skills, and for many, mathematics is a great addition. You can start machine learning without advanced mathematics, but at some point in your career, getting familiar with the mathematical background of machine learning can help you bring your skills to the next level.
In my opinion, there are two paths to mastery in deep learning. One starts from the practical parts, the other starts from theory. Both are perfectly viable, and eventually, they intertwine. This book is for those who started on the practical, application-oriented path, like data scientists, machine learning engineers, or even software developers interested in the topic.
This book is not a 100% pure mathematical treatise. At points, I will make some shortcuts to balance between clarity and mathematical correctness. My goal is to give you the “Eureka!” moments and help you understand the bigger picture instead of getting you ready for a PhD in mathematics.
Most machine learning books I have read fall into one of the two categories.
Focus on practical applications, unclear or imprecise with mathematical concepts.
Focus on theory, involving heavy mathematics with almost no real applications.
I want this book to offer the best of both: a sound introduction of basic and advanced mathematical concepts, keeping machine learning in sight at all times. My goal is not only to cover the bare fundamentals but to give a breadth of knowledge. In my experience, to master a subject, one needs to go both deep and wide. Covering only the very essentials of mathematics would be like a tightrope walk. Instead of performing a balancing act every time you encounter a mathematical subject in the future, I want you to gain a stable footing. Such confidence can bring you very far and set you apart from others.
During our journey, we are going to follow this roadmap. (You might need to zoom in, as the figure is relatively large.)
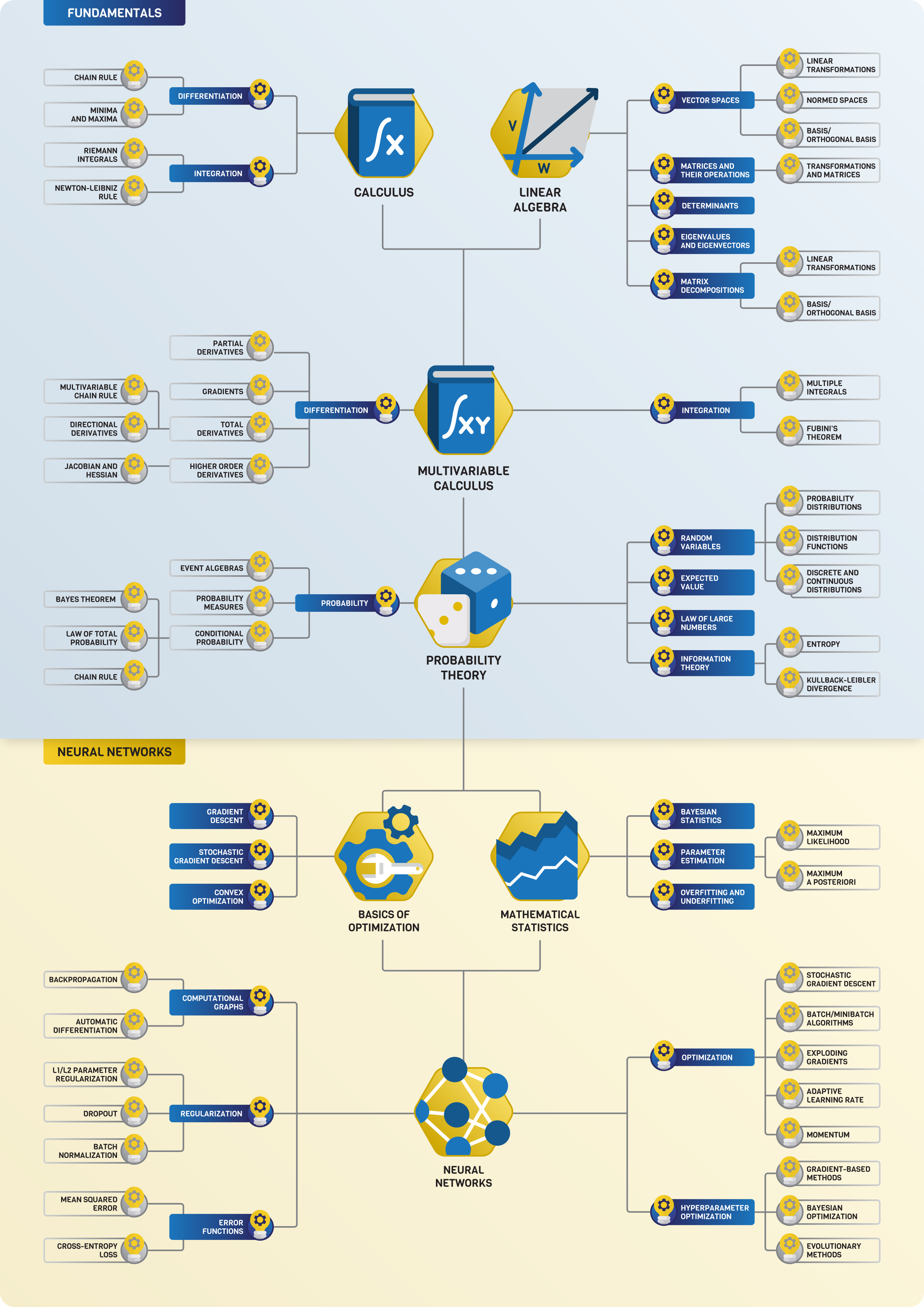
Fig. 1 The complete roadmap of mathematics for machine learning.¶
Before we start, let’s take a brief look into each part.
Linear algebra¶
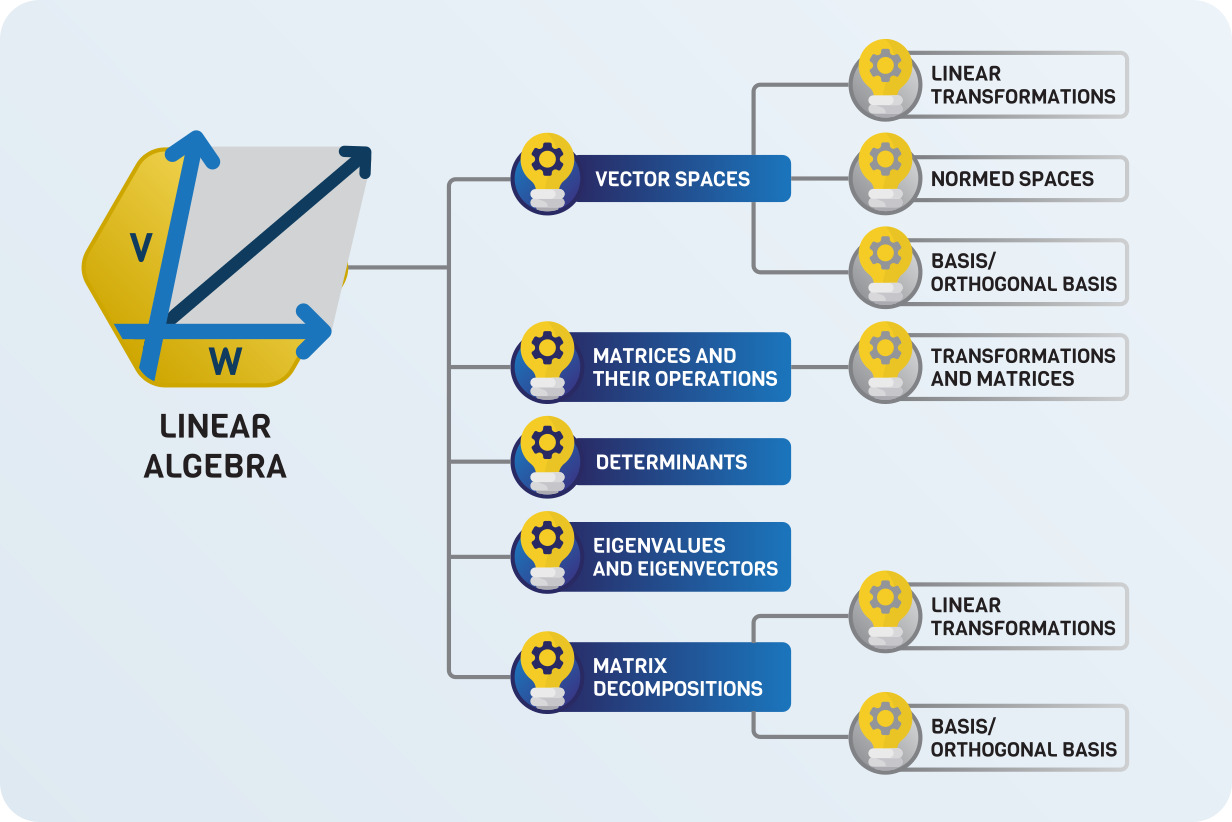
We are going to begin our journey with linear algebra. In machine learning, data is represented by vectors. Essentially, training a learning algorithm is finding more descriptive representations of data through a series of transformations.
Linear algebra is the study of vector spaces and their transformations.
Simply speaking, a neural network is just a function mapping the data to a high-level representation. Linear transformations are the fundamental building blocks of these. Developing a good understanding of them will go a long way, as they are everywhere in machine learning.
Calculus¶
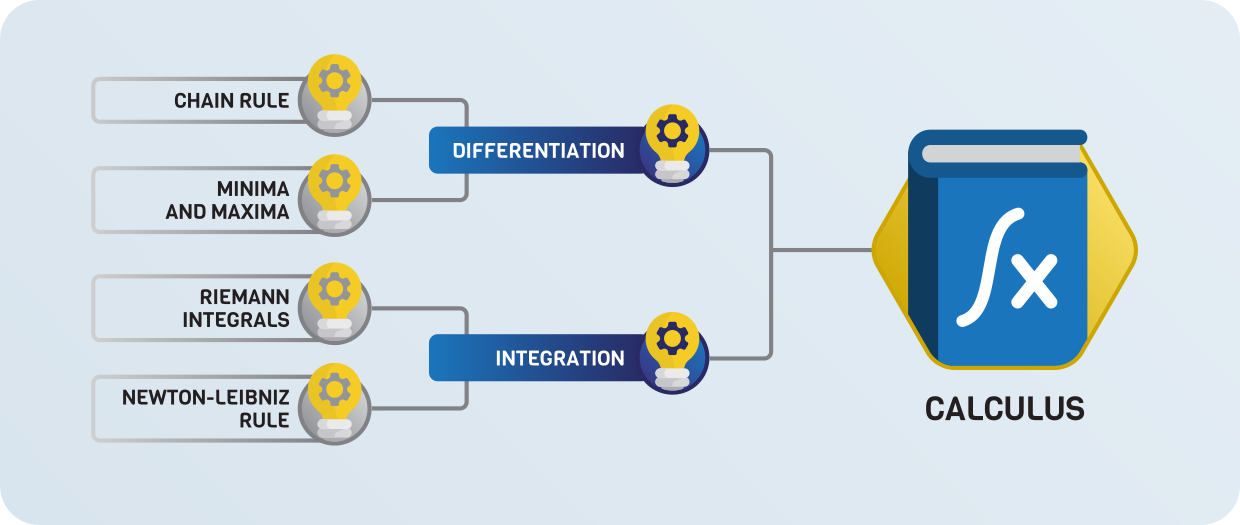
While linear algebra shows how to describe predictive models, calculus has the tools to fit them to the data. When you train a neural network, you are almost certainly using gradient descent, which is rooted in calculus and the study of differentiation.
Besides differentiation, its “inverse” is also a central part of calculus: integration.
Integrals are used to express essential quantities such as expected value, entropy, mean squared error, and many more. They provide the foundations for probability and statistics.
Multivariate calculus¶
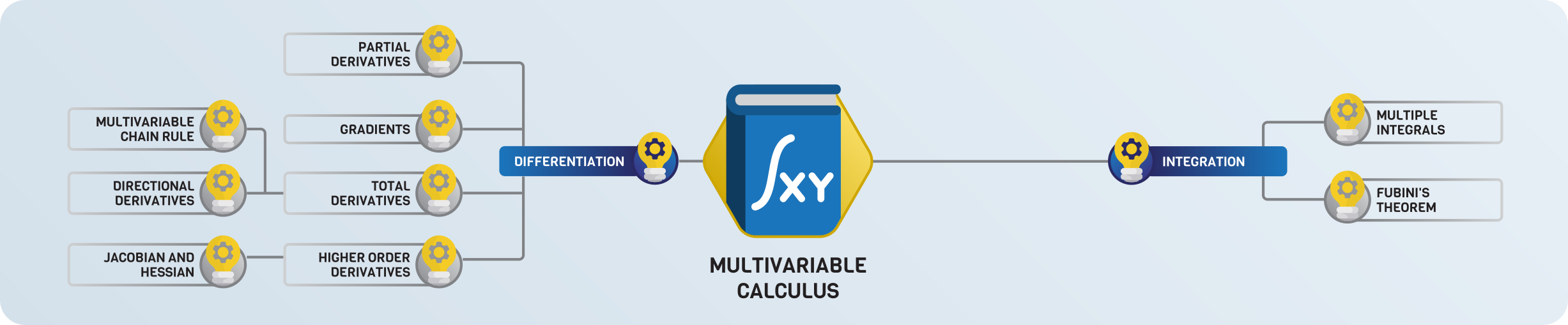
When doing machine learning, we deal with functions with millions of variables.
In higher dimensions, things work differently. This is where multivariable calculus comes in, where differentiation and integration are adapted to these spaces.
Probability theory¶
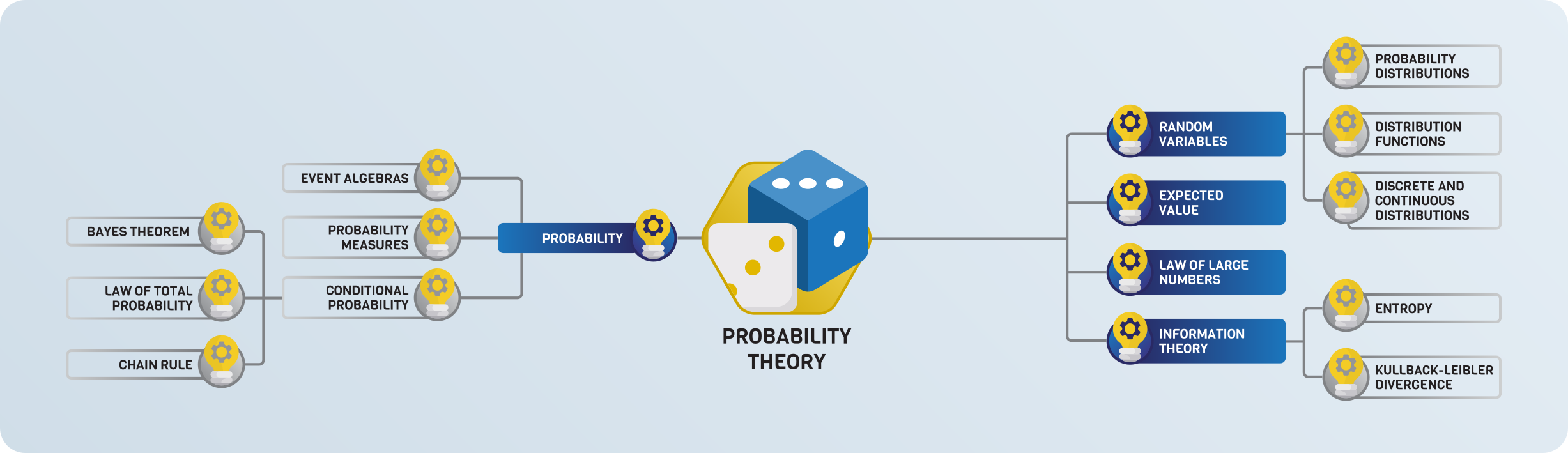
How to draw conclusions from experiments and observations? How to describe and discover patterns in them?
These are answered by probability theory and statistics, the logic of scientific thinking.
Beyond the fundamentals¶
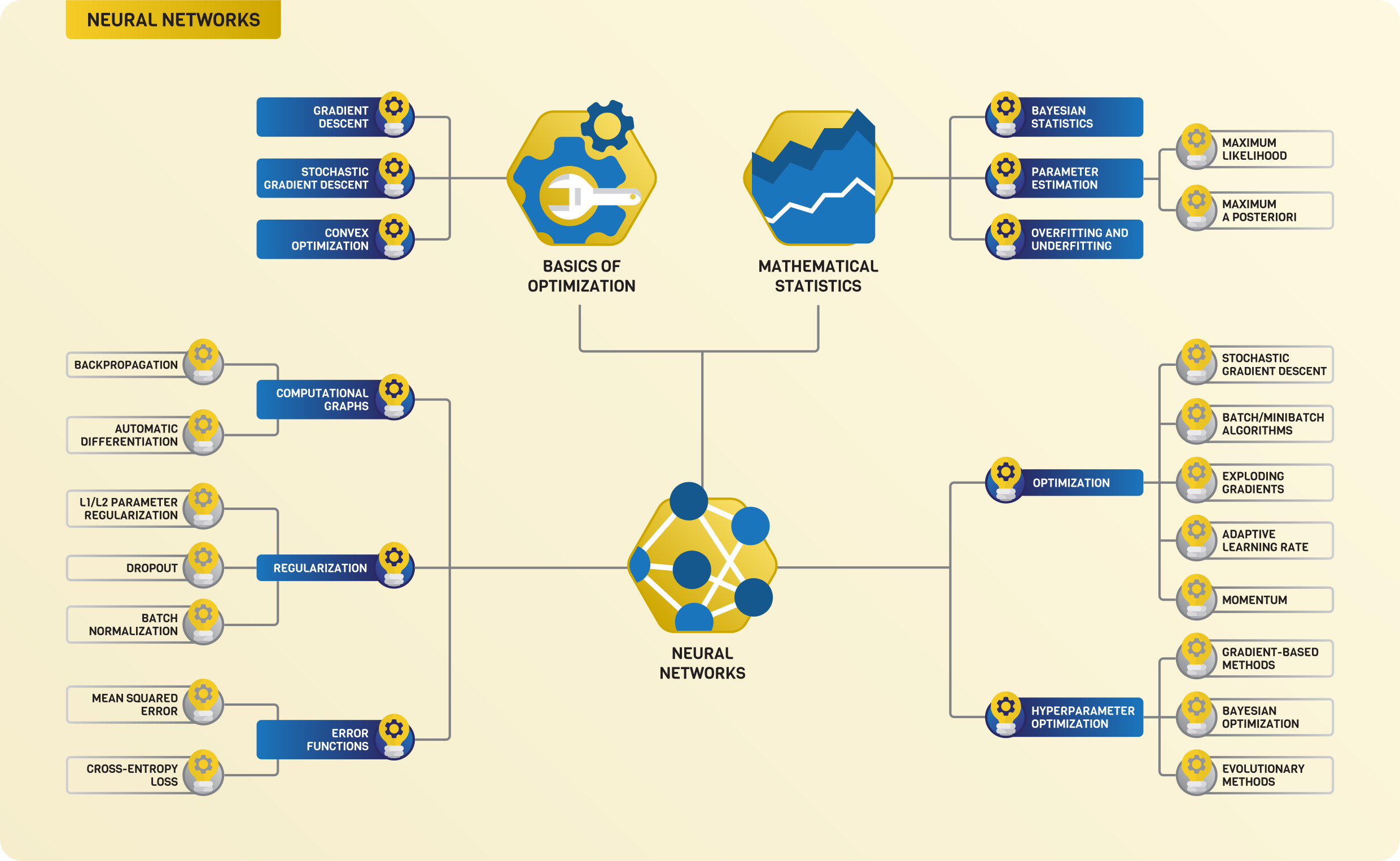
Linear algebra, calculus, and probability theory form the foundations of mathematics in machine learning. They are just the starting points. The most exciting stuff comes after we are familiar with them! Advanced statistics, optimization techniques, backpropagation, the internals of neural networks. In the second part of the book, we will take a detailed look at all of those.
How to read this book¶
Mathematics follows a definition-theorem-proof structure that might be difficult to follow at first. If you are unfamiliar with such a flow, don’t worry. I’ll give a gentle introduction right now.
In essence, mathematics is the study of abstract objects (such as functions) through their fundamental properties. Instead of empirical observations, mathematics is based on logic, making it universal. A correct mathematical result is set in stone, remaining valid forever. (Or, until the axioms of logic change.) If we want to use the powerful tool of logic, the mathematical objects need to be precisely defined. Definitions are presented in boxes like this below.
Definition 1 (An example definition.)
This is how definitions are presented in this book.
Given a definition, results are formulated as if A, then B statements, where A is the premise, and B is the conclusion. Such results are called theorems. For instance, if a function is differentiable, then it is also continuous. If a function is convex, then it has global minima. If we have a function, then we can approximate it with arbitrary precision using a single-layer neural network. You get the pattern. Theorems are the core of mathematics.
We must provide a sound logical argument to accept the validity of a proposition, one that deduces the conclusion from the premise. This is called a proof, responsible for the steep learning curve of mathematics. Contrary to other scientific disciplines, proofs in mathematics are indisputable statements, set in stone forever. On a practical note, look out for these boxes.
Theorem 1 (An example theorem.)
Let \( x \) be a fancy mathematical object. The following two statements hold.
(a) If \( A \), then \( B \).
(b) If \( C \) and \( D \), then \( E \).
Proof. This is where proofs go. \( \square \)
To enhance the learning experience, I’ll often make good-to-know but not absolutely essential information into remarks.
Remark 1 (An exciting remark.)
Mathematics is awesome. You’ll be a better engineer because of it.
The most effective way of learning is building things and putting theory into practice. In mathematics, this is the only way to learn. What this means to you is need to read through the text carefully. Don’t take anything for granted just because it is written down. Think through every sentence, take apart every argument and calculation. Try to prove theorems by yourself before reading the proofs.
